*This post accompanies a recent publication and is part of our
series story behind the paper,
inspired by [Jonathan Eisen’s series of the same
name](http://phylogenomics.blogspot.ch/search/label/story%20behind%20the%20paper).*
One fundamental step in sequence analysis is the identification of homologous
sequences, sequences related through common ancestry. There are many different
ways of identifying homolog but they broadly fall into two categories:
all-against-all comparisons and clustering.
The all-against-all approach aligns every sequence with every other one. This
is straighforward to implement, relatively sensitive, and robust to variations
in sequence lengths. The main downside of all-against-all comparisons is the
quadratic computational cost with respect to the number of sequences.
In contrast, clustering works by using one representative sequence or profile
per homologous family of genes (clusters), thus limiting the number of
required comparisons to one per cluster. Assuming a fixed (or nearly fixed)
number of clusters, the computational cost is (nearly) linear in the number of
input sequences. Clustering methods however tend to miss more homologous
relationships than the all-against-all.
Can the sensitivity of the all-against-all be achieved at the speed of clustering?
The OMA database—developed in our lab—currently
relies upon an all-against-all. With 8,798,758 protein sequences from 1706
genomes in the latest release, this represents 38.7 trillion alignments. We
could probably cope with a few thousands genomes more, but will struggle to
get to the next order of magnitude with the current pipeline.
Furthermore, it is difficult to accept that as we increasingly sample the protein
sequence universe, even though we know more and more about its diversity, the
marginal computational cost of adding sequences goes higher, not lower.
In this project, we thus set out to try to achieve the sensitivity of the
all-against-all at the speed of clustering.
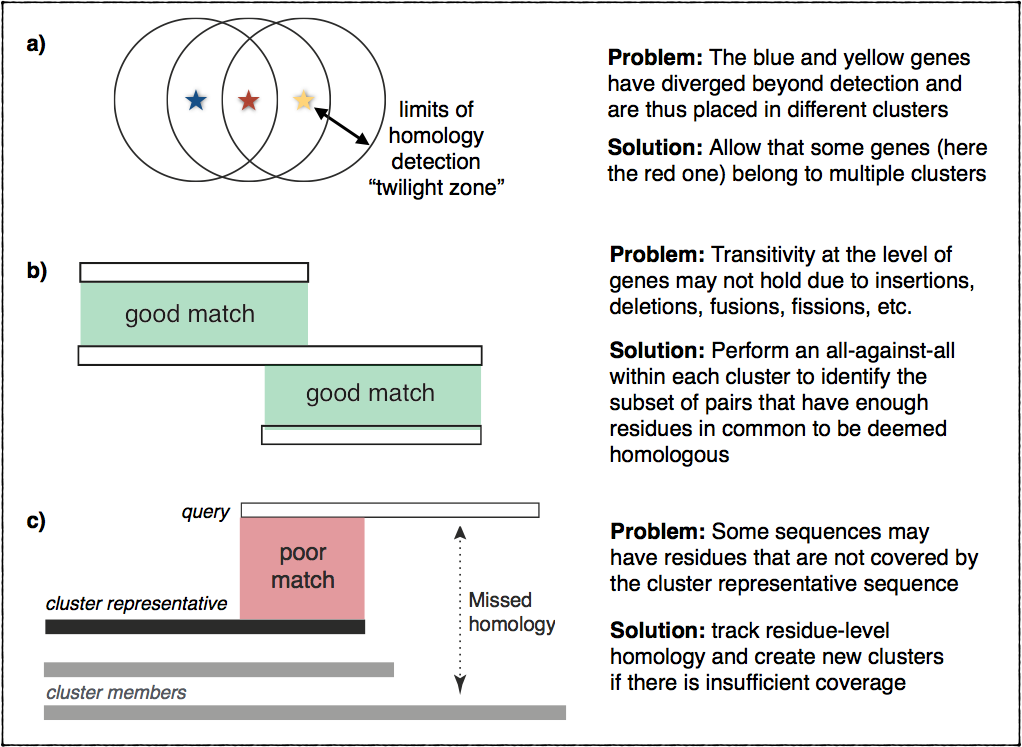
Transitivity of homology
In principle, homology is a transitive relationship: if gene A is homologous
to gene B, and gene B is homologous to gene C, this implies that gene A is
homologous to gene C. Transitive relationships are typically a good fit for
clustering.
In practice, however, things are more complicated. Homology can be difficult
to ascertain for very divergent sequences. Furthermore, homology is not always
transitive due to insertions, deletions, fusion, fissions, and other events
that may cause inconsistencies in terms of matching residues across multiple
homologs. This figure illustrates these problems and outlines the ideas
we implemented to address them:
Encouraging results
Putting together the ideas outlined in the figure above, we were pleasantly
surprised to see that clustering can indeed be both sensitive and fast. We
obtained 4-5x speed-ups across various datasets while recovering ~99.9% of all
homologous relationships identified through all-against-all.
In comparison, general purpose clustering approaches such as
kClust or
UCLUST—which [admittedly have not been
designed to identify distant homologs
effectively](http://drive5.com/usearch/manual/uclust_algo.html)—only recover
~10% of all homologous relationships. They are, however, several orders of
magnitude faster.
Only the beginning
The results of our proof-of-concept implementation are thus very
encouraging. We have plans to follow up with a long list of refinement ideas,
many of which we discuss in the manuscript. One essential
refinement will be to parallelise the new approach. This is not as
straightforward as with all-against-all compraisons, but we think it can be
done.
Meanwhile, the serial variant is available as part of the [OMA
standalone](http://omabrowser.org/standalone) package.
Reference
Wittwer, L., Piližota, I., Altenhoff, A., & Dessimoz, C. (2014). Speeding up all-against-all protein comparisons while maintaining sensitivity by considering subsequence-level homology PeerJ, 2:e607 DOI: 10.7717/peerj.607